Sleep deprivation impairs learning and memory, but now is the time for replication science.
- Rebecca Crowley

- Mar 17, 2022
- 5 min read
Research has long suggested that sleep is critical for learning and memory. Sleep after learning strengthens new memories and redistributes them from short-term to long-term memory stores. Sleep before learning restores learning capacity for the day ahead. Despite this, sleep deprivation is prevalent in modern society: think of students with their preference for eveningness as well as shift work in medical and industrial workers to name a few. So, what are the consequences of missing one or more nights of sleep for learning and memory? We recently published two meta-analytic reviews of studies on sleep deprivation before and after learning to address these issues.
What did we find?
We collected data across 5 decades of research and extracted 31 reports (55 effect sizes, 927 participants) investigating effects of sleep deprivation before learning, and 45 reports (130 effect sizes, 1,616 participants) investigating effects of sleep deprivation after learning.
The results were clear: Missing a night of sleep before learning impairs memory (g = 0.62; medium-to-large effect size) and so does missing a night of sleep after learning (g = 0.28; small-to-medium effect size).
Forest plots containing effect sizes and 95% confidence intervals for the sleep deprivation before learning meta-analysis (left) and the sleep deprivation after learning meta-analysis (right).
But that isn’t the full story.
There is growing concern that the resource-intensive nature of sleep research exacerbates issues of low power and publication bias in this field. Both of these problems are non-trivial for meta-analytic estimates because they increase the likelihood that effect sizes in the literature are exaggerated and that effects reported as significant are false positives. Therefore, we investigated the extent to which these problems characterise the last 50 years of sleep deprivation research. Unfortunately, the results were again clear.
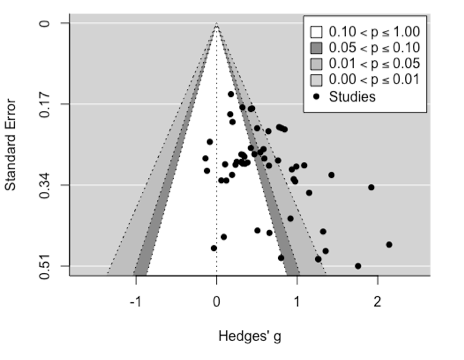
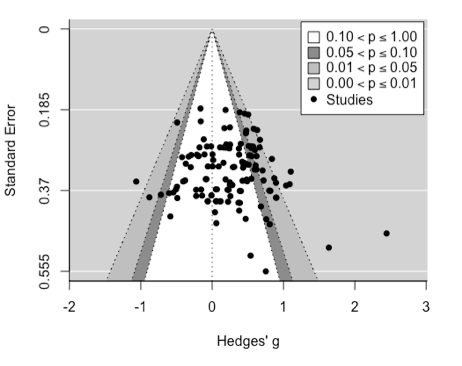
Publication bias is evident when published findings disproportionately align with hypotheses and there are few published studies reporting non-significant results. This is called the ‘file drawer’ problem. Across our meta-analyses, it was clear that studies reporting a detrimental effect of sleep deprivation are published more often than those finding no effect of sleep deprivation, and there were sleep deprivation before learning studies missing from the non-significance zones. Further, when standard errors are highest, and therefore the precision of the effect size is most questionable, the literature favours large, positive effect sizes.
Funnel plots displaying effect sizes according to standard error for the sleep deprivation before learning meta-analysis (left) and the sleep deprivation after learning meta-analysis (right).
We quantified the impact of publication bias by estimating the missing effect sizes and then adjusting the overall meta-analytic estimates. These calculations revealed that the true effect size of sleep deprivation before learning on memory is more likely around g = 0.46 and the effect size of sleep deprivation after learning is more likely around g = 0.17.
Crucially, both adjusted effect sizes are still significantly above 0. Sleep deprivation before and after learning does still impair memory. But, sleep scientists (and reviewers, and editors) should recognise that publication bias in this field is causing the average effect size to be overestimated by 35-65%. This is particularly concerning given that the adjusted meta-analytic estimate for the effect of sleep deprivation after learning no longer crosses Cohen’s guidelines for a small effect size. Some would argue it therefore has limited real-world importance.
Unpublished studies are not the only problem.
When an effect size is small, a large number of participants (greater statistical power) is needed to detect it. Poorly powered studies have sample sizes that are smaller than would be required to detect the effect size in question. The agreed upon convention is that a study should have enough participants to achieve 80% statistical power.
Poorly powered studies increase uncertainty around true effect sizes and they can lead to overestimates in the meta-analytic effect size in three ways. First, these studies may fail to detect an effect and remain in the file drawer because of publication bias. Second, a detected effect in a poorly powered study will by definition have an inflated effect size; otherwise it would not have reached statistical significance. Third, there is a greater chance that the detected effect is a false positive. We wanted to probe how confident we could be in our average meta-analytic estimates based on whether the included studies had sufficient statistical power.
To do this, we calculated the statistical power of each experiment included in the meta-analyses to detect our meta-analytic estimates of g = 0.62 and g = 0.28 for sleep deprivation before and after learning, respectively. Statistical power did not moderate the sleep deprivation effect. In other words, it was not the case that detrimental effects of sleep deprivation were found only in the smallest and most imprecise studies. Rather, similar effect sizes were found across all sample sizes. However, studies investigating sleep deprivation after learning had a mean statistical power of just 14% (range: 7-30%). The mean statistical power achieved in studies investigating sleep deprivation before learning was much greater at 55% (range: 21-98%). This is reassuring but also unsurprising given that this effect size estimate was more than twice as large as the sleep deprivation after learning estimate and therefore fewer participants are needed to achieve greater statistical power. Note also that achieved statistical power would be much lower in both meta-analyses if studies needed to be powered to detect the smaller effect sizes adjusted for publication bias.
Density plots showing the distribution of power to find the mean meta-analytic effect sizes for the sleep deprivation before learning meta-analysis (left) and the sleep deprivation after learning meta-analysis (right).
To be clear, the issue of statistical power that we have highlighted here is not a criticism unique to the sleep deprivation literature. In cognitive neuroscience and psychology more generally, the mean power to detect small and medium effect sizes (17% and 49% respectively) is in line with what we found here. But this does not mean that we should accept the status quo.
What next?
We argue that there is a need to move from original to replication science (Wilson et al., 2020) at this point.
Original science is the science we know and love. Often poorly-powered designs but which serve as an inexpensive screening function to identify effects that warrant further investigation. This is where replication science comes in. Replication science is the gold standard, highly-powered, expensive studies which verify findings from original science.
Moving to replication science in sleep research will require a shift in the bodies that fund it. A study investigating sleep deprivation after learning would need as many as 410 participants to achieve 80% power in a between-subjects design. If a PhD application or a research grant proposes one such properly-powered sleep study over the next three years, would it get funded? Probably not. It is slow and expensive. Yet, without these high-quality studies we are left with a scientific effort of over 50 years, thousands of participants, and likely tens of millions of pounds that has left uncertainty in the sizes of these effects.
Our meta-analyses show that sleep deprivation, both before and after learning, impairs memory. However, properly powered, pre-registered replications are needed to verify the sizes of these effects.
Newbury, C. R., Crowley, R., Rastle, K., & Tamminen, J. (2021). Sleep deprivation and memory: Meta-analytic review of studies on sleep deprivation before and after learning. Psychological Bulletin, 147(11), 1215-1240. https://doi.org/10.1037/bul0000348 #OpenAccess













Comments